6.0 Lession 6 明暗处理
[TOC]
明暗处理
浓淡处理(英语:Shading,也称明暗处理、着色法)是在三维模型或插画中通过不同的亮度表现深度的方法。
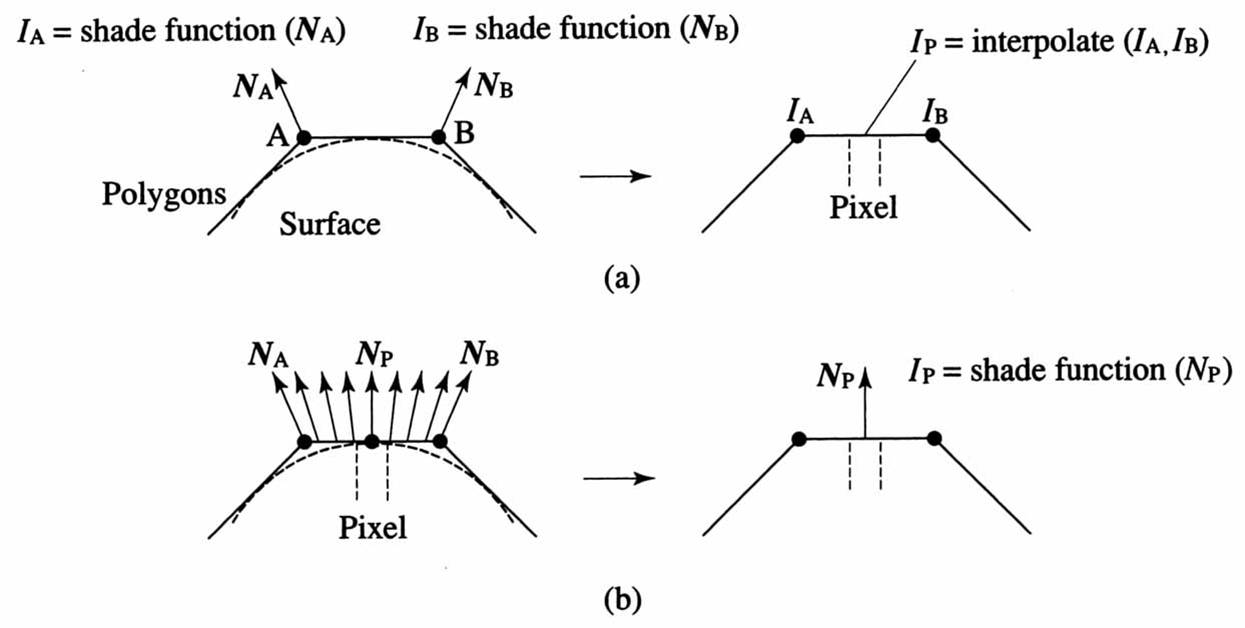
渲染过程中需要计算表面的亮度,上述光照模型要求我们提前知道表面上任意点的法线。然而,三维模型一般都是通过多边形网格描述的,只能在有限的点存储法线,这些点通常是多边形的顶点。为了解决这一问题,可以使用不同的插值技术。
平直着色法 Flat shading
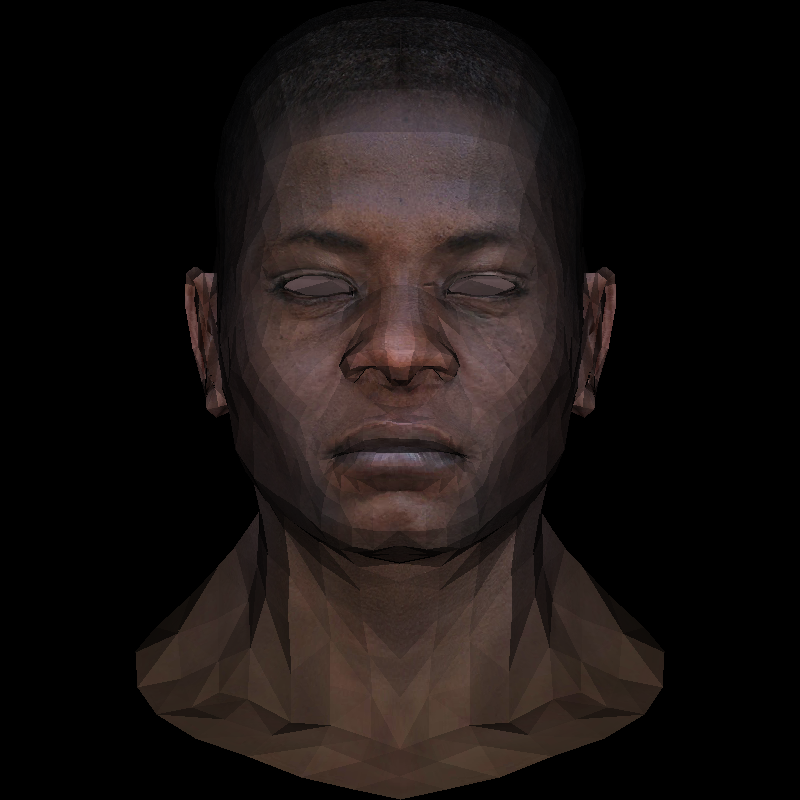
只计算一个顶点的法线,然后通过法线和光照向量的数量积得到系数,一个三角形都使用这个明暗系数,可以看到格子很明显
计算很简单,但是效果比较差
平直着色法(英语:flat shading)基于“组成模型的多边形都是平的”的假设,认为在同一多边形上任意点的法线都相同。
使用这种着色法时,先在每个多边形上挑选一个点计算颜色(通常是多边形的第一个顶点,如果是三角形网格则也可以选择几何中心),则该多边形上其余点都直接使用该点的颜色。所以,使用平直着色法的每个多边形上都是统一的颜色,和最近邻插值的效果类似。
其它更加高级的着色技术由于计算量太大不便于使用时,这种方法经常用于高速渲染。由于每个多边形都是统一的颜色,所以使用这种着色法也更易于区分相邻的多边形。但这种着色法很难做出高光效果:一个表面要不全高光,要不全没有,因此高光模型很少使用在这个着色方法中。
for (int i=0; i<model->nfaces(); i++) {
std::vector<int> face = model->face(i);
Vec3i screen_coords[3];
Vec3f world_coords[3];
for (int j=0; j<3; j++) {
Vec3f v = model->vert(face[j]);
screen_coords[j] = Vec3i((v.x+1.)*width/2., (v.y+1.)*height/2., (v.z+1.)*depth/2.);
world_coords[j] = v;
}
Vec3f n = (world_coords[2]-world_coords[0])^(world_coords[1]-world_coords[0]);
n.normalize();
float intensity = n*light_dir;
if (intensity>0) {
Vec2i uv[3];
for (int k=0; k<3; k++) {
uv[k] = model->uv(i, k);
}
std::cout<<"instensity = " << intensity << "\n";
triangle_texture(screen_coords[0], screen_coords[1], screen_coords[2], uv[0], uv[1], uv[2], image, intensity, zbuffer);
}
}

平滑着色法
使用平直着色法时,颜色在多边形的边缘跳变。而使用平滑着色法(英语:smooth shading)时,每个像素的颜色都可以不同,相邻多边形之间的颜色转变看上去就比较平滑。通常先计算多边形顶点的颜色,再通过双线性插值来确定多边形上其它点的像素值。
Gouraud shading

工作原理
- 计算多边形的顶点法向量
- 顶点法向量能被直接计算(如均一网格上的高度图)
- 可能相邻面的法向量的加权平均

- 用光照模型去计算每个顶点的光强,例如Phong reflection model
- 用双线性插值计算多边形表面上每个像素的明暗
Gouraud shading is really simple. Our kind 3d artists gave us normal vectors to each vertex of the model, they can be found in "vn x y z" lines of the .obj file. We compute the intensity per vertex (and not per triangle as before for the flat shading) and then simply interpolate the intensity inside each triangle as we already did for z or uv coordinates.
struct GouraudShader : public IShader {
Vec2i varying_uv[3];
Vec3f varying_inty;
virtual Vec3i vertex(int iface, int nthvert) {
varying_inty[nthvert] = std::max(0.f, model->norm(iface, nthvert) * light_dir);
varying_uv[nthvert] = model->uv(iface, nthvert);
Vec3f gl_Vertex = model->vert(iface, nthvert);
Vec3i gl_Position = vf2i(m2v(Viewport * Projection * ModelView * Matrix(gl_Vertex)));
return gl_Position;
}
virtual bool fragment(Vec3f bar, TGAColor &color) {
Vec2i uv = varying_uv[0] * bar.x + varying_uv[1] * bar.y + varying_uv[2] * bar.z;
/**
* 实际上是利用顶点法线计算光强度,然后插值,乘以纹理计算后的颜色
*/
float inty = varying_inty[0] * bar.x + varying_inty[1] * bar.y + varying_inty[2] * bar.z;
inty = std::max(0.f, std::min(1.f, inty));
color = model->diffuse(uv) * inty;
return false;
}
}
优缺点
Gouraud着色法的优势在于,即便是比三角形复杂的多边形,每个顶点也可以有不一样的颜色,内部插值算法可以更多变。
而Gouraud着色法也有一些问题:
- 邻接多边形可能有不一样的颜色。
- Gouraud着色 需要比较大的CPU计算量,在实时处理大量多边形时可能会成为问题。
3个多边形边的T型连接可能会被错误的绘制,一般来说应该避免存在T型连接
Phong shading
Phong着色法与Gouraud着色法类似,区别在于进行双线性插值的不是光照强度本身,而是顶点的法线。因此使用这种着色法计算出的高光比Gouraud着色更精确。
- 计算多边形顶点的法向量
- 双线性插值计算每个像素点的法向量
- 通过每个像素的法向量计算光强
- 根据光强绘制像素

struct PhongShader : public IShader {
Vec2i varying_uv[3];
Vec3f varying_norm[3];
virtual Vec3i vertex(int iface, int nthvert) {
varying_norm[nthvert] = model->norm(iface, nthvert);
varying_uv[nthvert] = model->uv(iface, nthvert);
Vec3f gl_Vertex = model->vert(iface, nthvert);
Vec3i gl_Position = vf2i(m2v(Viewport * Projection * ModelView * Matrix(gl_Vertex)));
return gl_Position;
}
virtual bool fragment(Vec3f bar, TGAColor &color) {
Vec2i uv = varying_uv[0] * bar.x + varying_uv[1] * bar.y + varying_uv[2] * bar.z;
Vec3f bn = Vec3f(
varying_norm[0].x * bar.x + varying_norm[1].x * bar.y +varying_norm[2].x * bar.z,
varying_norm[0].y * bar.x + varying_norm[1].y * bar.y +varying_norm[2].y * bar.z,
varying_norm[0].z * bar.x + varying_norm[1].z * bar.y +varying_norm[2].z * bar.z
);
bn.normalize();
float inty =std::max(0.f, bn * light_dir);
color = model->diffuse(uv) * inty;
return false;
}
};
Gouraud shading和Phong shading的不同
- Gouraud对顶点颜色赋值,然后双线性插值计算颜色,Phong都某个点的法向量进行线性插值,从而计算光照强度
~- Gouraud更快,计算量更小,但是高光和镜面效果不好