FengBo`s Blog

温故而知新

列表 标签 归档 关于

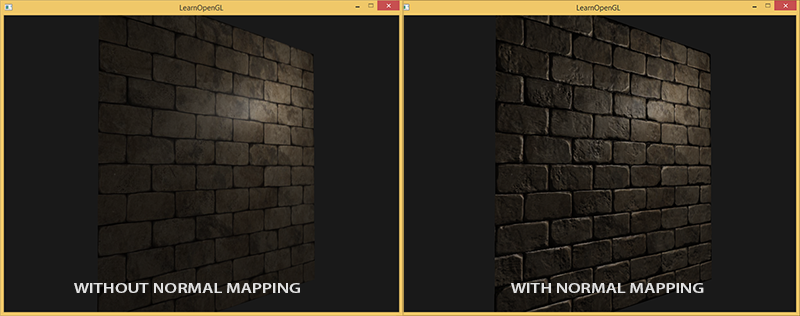
6.2 Lession 6 法线贴图和Tangent空间

2020-10-13 6 min read # 渲染引擎

[TOC]

bump mapping 凹凸贴图

凹凸贴图（bump mapping），又称为凸凹纹理映射、皱面贴图，是一项计算机图形学技术，在这项技术中每个待渲染的像素在计算照明之前都要加上一个从高度图中找到的扰动。这样得到的结果表面表现更加丰富、细致，更加接近物体在自然界本身的模样。法线贴图是一项常用的凹凸贴图技术，另外还有许多其它的实现技术，如视差映射等等。

不带凹凸贴图的球体;下图所用的凸凹纹理;这个使用凹凸贴图的球体几何上与上面的球体一模一样，这改变了球体的浓淡效果，使它看起来像一个橙。

Normal mapping 法线贴图

法线贴图通常以普通RGB图像的形式存储，其中的R、G、B分量分别对应法线的X、Y、Z坐标。

  • X: -1 ~ +1 : 红: 0 ~ 255

  • Y: -1 ~ +1 : 绿: 0 ~ 255

  • Z: 0 ~ -1 : 蓝: 128 ~ 255(假设z范围是[0,1])

  • 直接指向观察者的法线 (0,0,-1) 映射为 (128,128,255)。所以（法线所创造的凹凸）物体上直接面朝观察者的部分为浅蓝色，也是法线贴图上最常见的颜色。

  • 指向纹理右上角的法线 (1,1, 0) 映射为 (255,255,128)。所以物体的右上角一般是浅黄色，也是颜色贴图上最亮的部分。

  • 指向纹理右侧的法线 (1,0,0) 映射为 (255,128,128)。所以物体的右边一般是浅红色。

  • 指向纹理顶部的法线 (0,1,0) 映射为 (128,255,128)。所以物体的顶边一般是浅绿色。

  • 指向纹理左侧的法线 (-1,0,0) 映射为 (0,128,128)。所以物体的左边一般是深蓝绿色。

  • 指向纹理底部的法线 (0,-1,0) 映射为 (128,0,128)。所以物体的底边一般是深杨红色。

  • 指向纹理左下角的法线 (-1,-1,0) 映射为 (0,0,128)。所以物体的左下角一般是深蓝色，也是颜色贴图上最暗的部分。


Tangent Space 切空间

learnopengl-法线贴图-切线空间

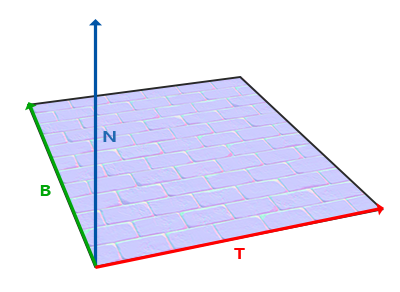
基于RGB颜色的法线贴图无法适用于物体发生旋转等变换，因为得到的法线值是固定方向的，所以需要引入切空间

法线贴图中的法线向量定义在切线空间中，法线永远指着正z方向。切线空间是位于三角形表面之上的空间：法线相对于单个三角形的本地参考框架。它就像法线贴图向量的本地空间；它们都被定义为指向正z方向，

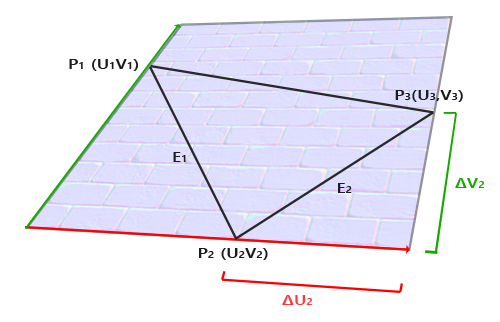
切线空间的计算




// positions
glm::vec3 pos1(-1.0,  1.0, 0.0);
glm::vec3 pos2(-1.0, -1.0, 0.0);
glm::vec3 pos3(1.0, -1.0, 0.0);
glm::vec3 pos4(1.0, 1.0, 0.0);
// texture coordinates
glm::vec2 uv1(0.0, 1.0);
glm::vec2 uv2(0.0, 0.0);
glm::vec2 uv3(1.0, 0.0);
glm::vec2 uv4(1.0, 1.0);
// normal vector
glm::vec3 nm(0.0, 0.0, 1.0);


glm::vec3 edge1 = pos2 - pos1;
glm::vec3 edge2 = pos3 - pos1;
glm::vec2 deltaUV1 = uv2 - uv1;
glm::vec2 deltaUV2 = uv3 - uv1;

GLfloat f = 1.0f / (deltaUV1.x * deltaUV2.y - deltaUV2.x * deltaUV1.y);

tangent1.x = f * (deltaUV2.y * edge1.x - deltaUV1.y * edge2.x);
tangent1.y = f * (deltaUV2.y * edge1.y - deltaUV1.y * edge2.y);
tangent1.z = f * (deltaUV2.y * edge1.z - deltaUV1.y * edge2.z);
tangent1 = glm::normalize(tangent1);

bitangent1.x = f * (-deltaUV2.x * edge1.x + deltaUV1.x * edge2.x);
bitangent1.y = f * (-deltaUV2.x * edge1.y + deltaUV1.x * edge2.y);
bitangent1.z = f * (-deltaUV2.x * edge1.z + deltaUV1.x * edge2.z);
bitangent1 = glm::normalize(bitangent1);  

[...] // 对平面的第二个三角形采用类似步骤计算切线和副切线

切线空间法线贴图

#version 330 core
layout (location = 0) in vec3 position;
layout (location = 1) in vec3 normal;
layout (location = 2) in vec2 texCoords;
layout (location = 3) in vec3 tangent;
layout (location = 4) in vec3 bitangent;

void main()
{
   [...]
   vec3 T = normalize(vec3(model * vec4(tangent,   0.0)));
   vec3 B = normalize(vec3(model * vec4(bitangent, 0.0)));
   vec3 N = normalize(vec3(model * vec4(normal,    0.0)));
   mat3 TBN = mat3(T, B, N)
}

  • 1.我们直接使用TBN矩阵，这个矩阵可以把切线坐标空间的向量转换到世界坐标空间。因此我们把它传给片段着色器中，把通过采样得到的法线坐标左乘上TBN矩阵，转换到世界坐标空间中，这样所有法线和其他光照变量就在同一个坐标系中了。

    normal = texture(normalMap, fs_in.TexCoords).rgb;
normal = normalize(normal * 2.0 - 1.0);   
normal = normalize(fs_in.TBN * normal);

有了TBN矩阵我们现在就可以更新法线贴图代码，引入切线到世界空间变换：

  • 2.我们也可以使用TBN矩阵的逆矩阵，这个矩阵可以把世界坐标空间的向量转换到切线坐标空间。因此我们使用这个矩阵左乘其他光照变量，把他们转换到切线空间，这样法线和其他光照变量再一次在一个坐标系中了。

法线坐标转换

(Projection*ModelView).inverse().transpose()

参考

Powered by Gridea RSS