Appendix:数学基础
[TOC]
线性插值算法
最近邻插值
线性插值
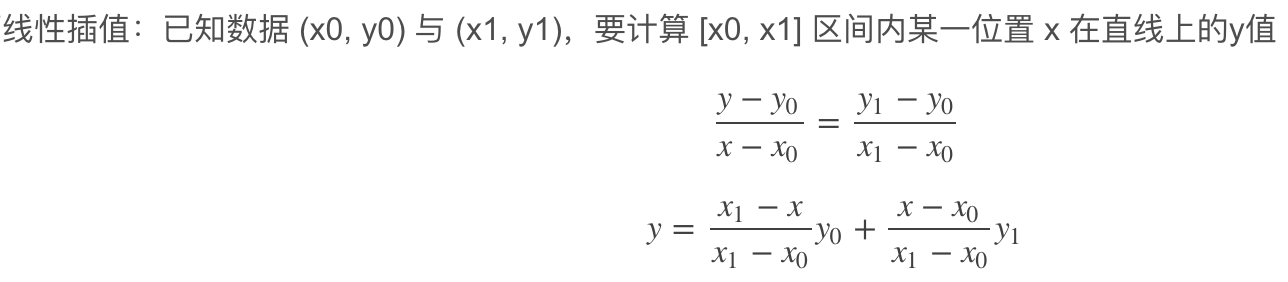
双线性插值
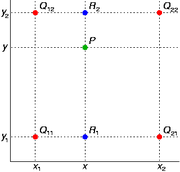
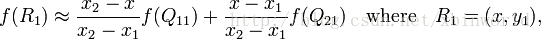
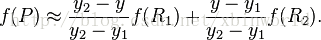
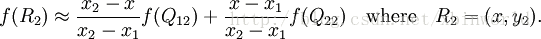
基 (线性代数)
https://zh.wikipedia.org/wiki/%E5%9F%BA_(%E7%B7%9A%E6%80%A7%E4%BB%A3%E6%95%B8)
点积和叉积
点积
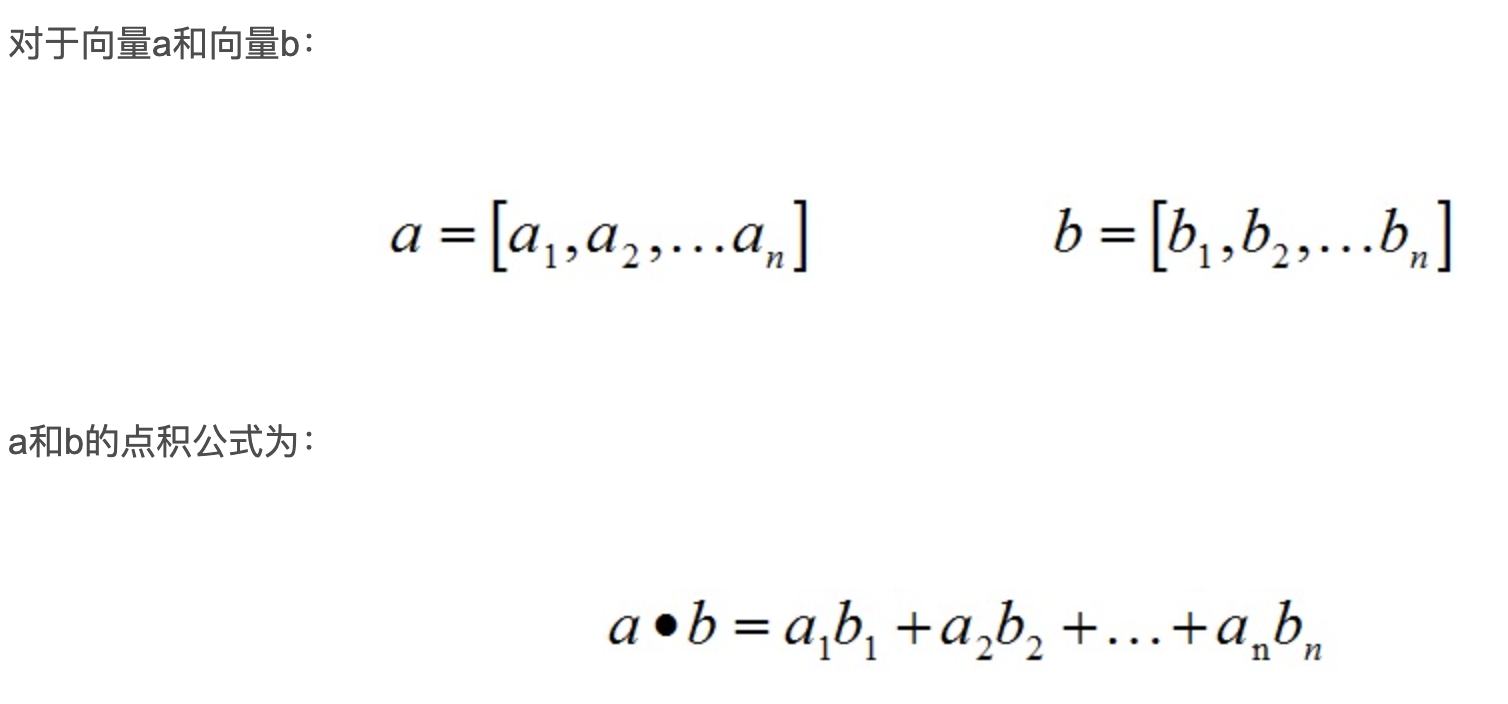
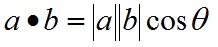
几何意义
计算向量夹角
几何意义
-
表征或计算两个向量之间的夹角
- a·b>0 方向基本相同,夹角在0°到90°之间
- a·b=0 正交,相互垂直
- a·b<0 方向基本相反,夹角在90°到180°之间
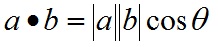
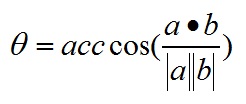
-
b向量在a向量方向上的投影
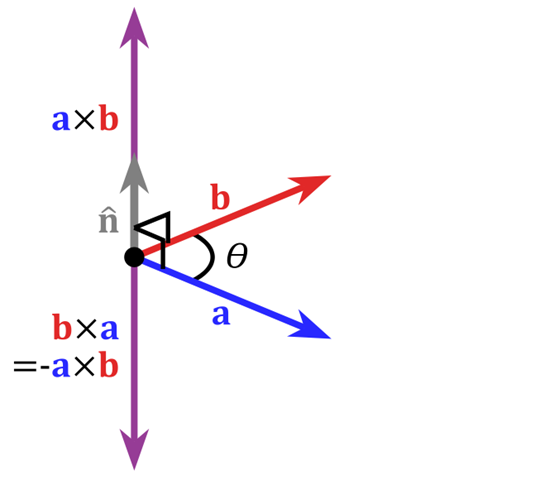
叉积
两个向量的叉乘,又叫向量积、外积、叉积,叉乘的运算结果是一个向量而不是一个标量。并且两个向量的叉积与这两个向量组成的坐标平面垂直。
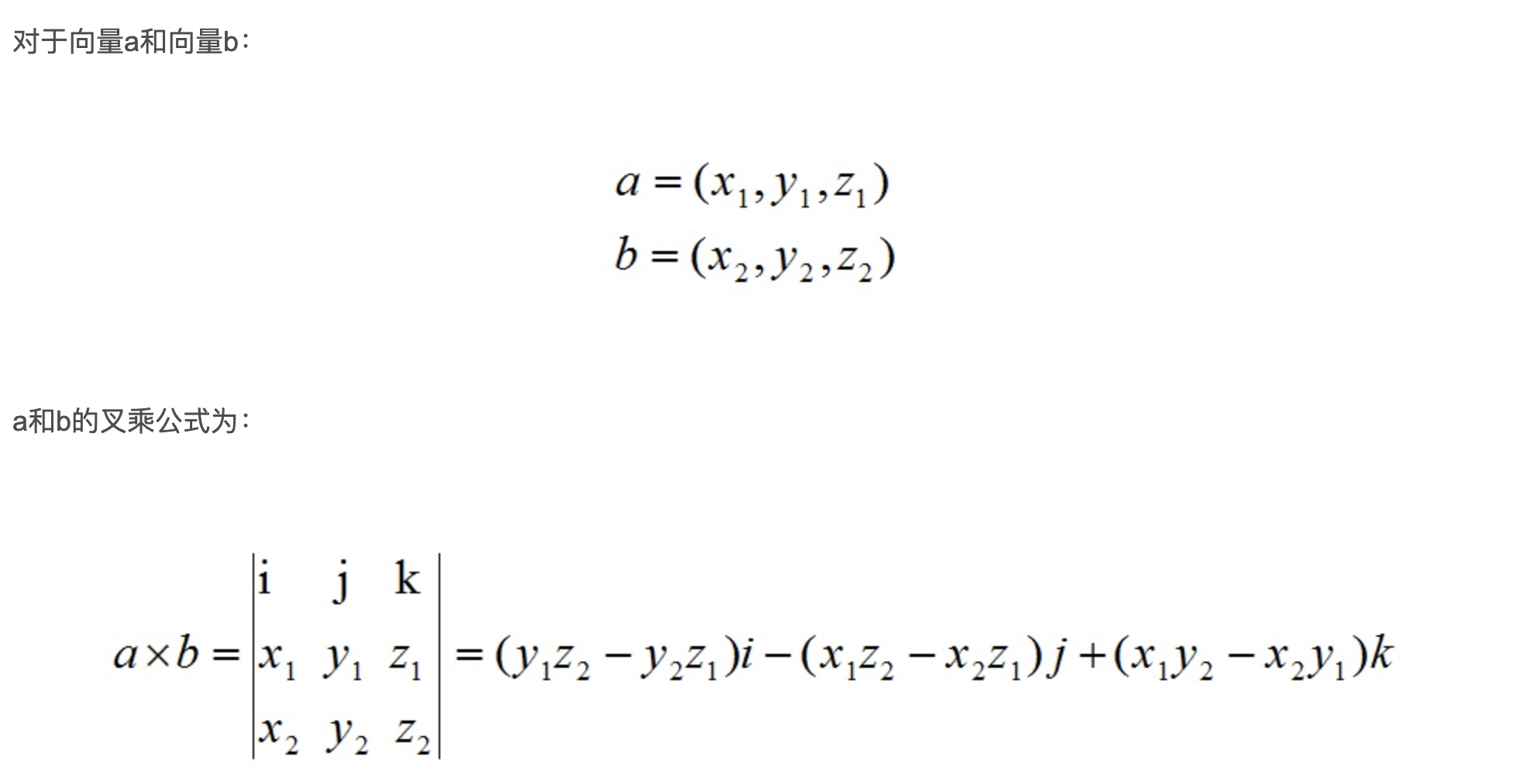
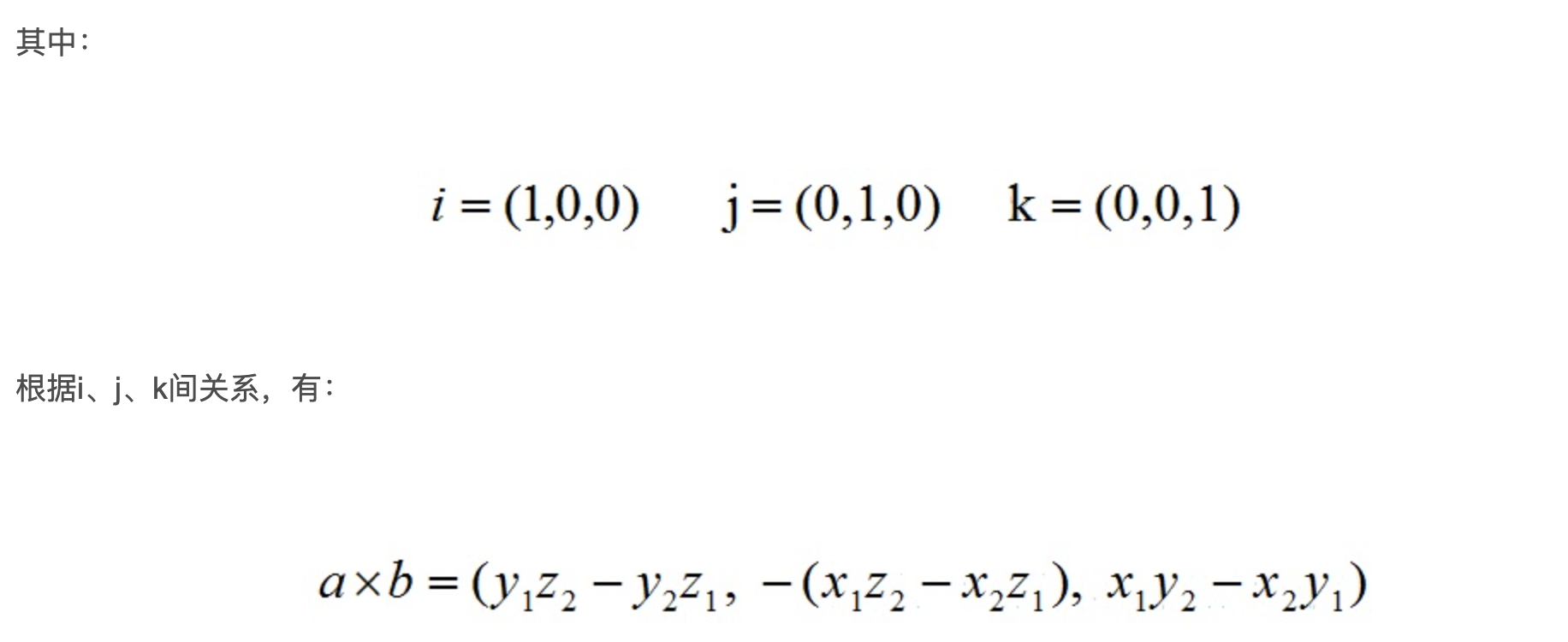
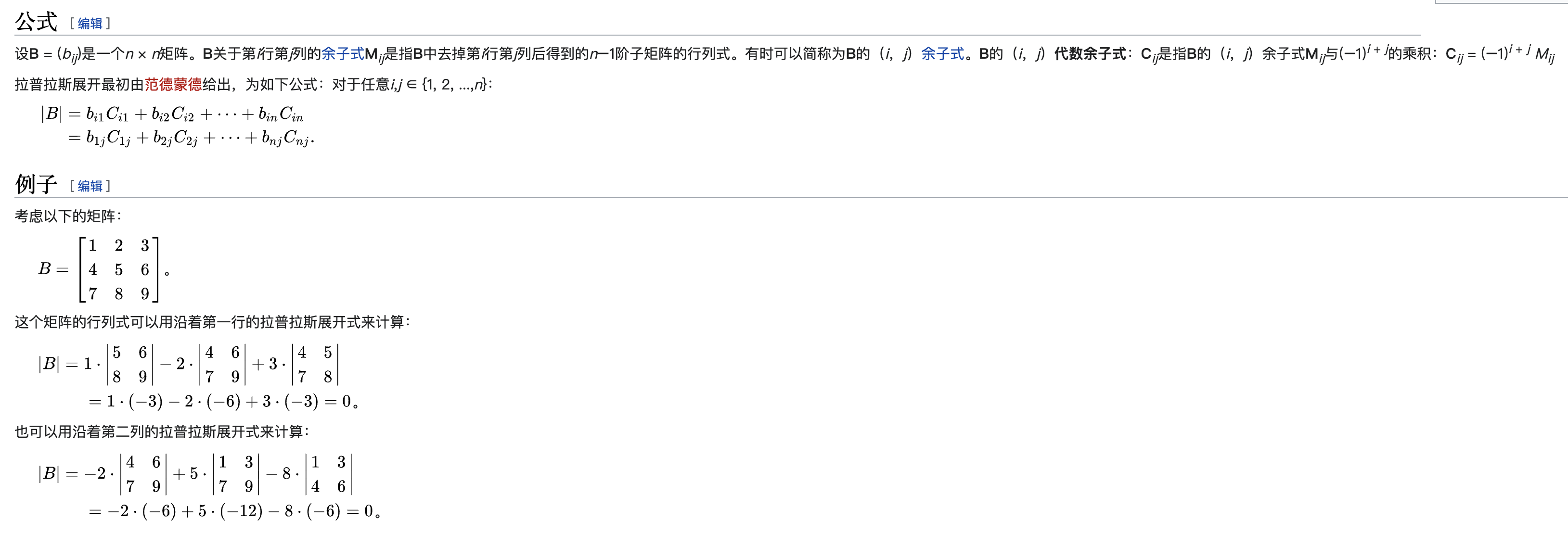
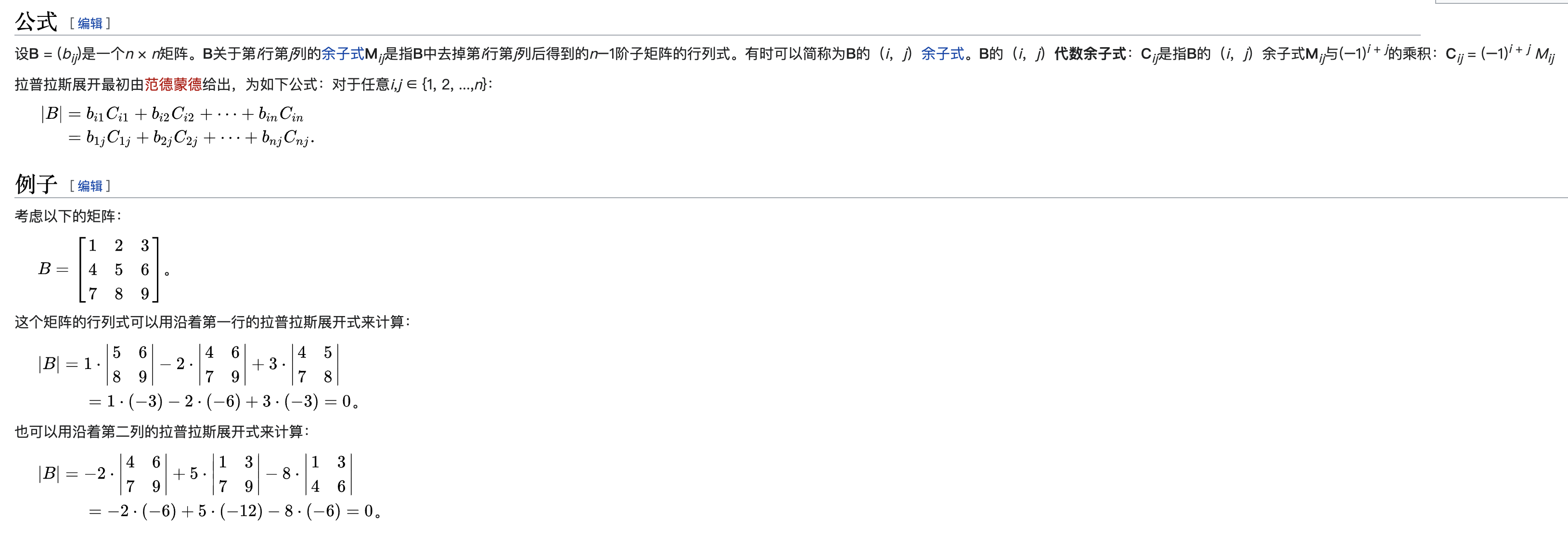
如果对导出公式有疑问可以参考拉普拉斯展开式:
几何参考:
在三维几何中,向量a和向量b的叉乘结果是一个向量,更为熟知的叫法是法向量,该向量垂直于a和b向量构成的平面。

拉普拉斯展开
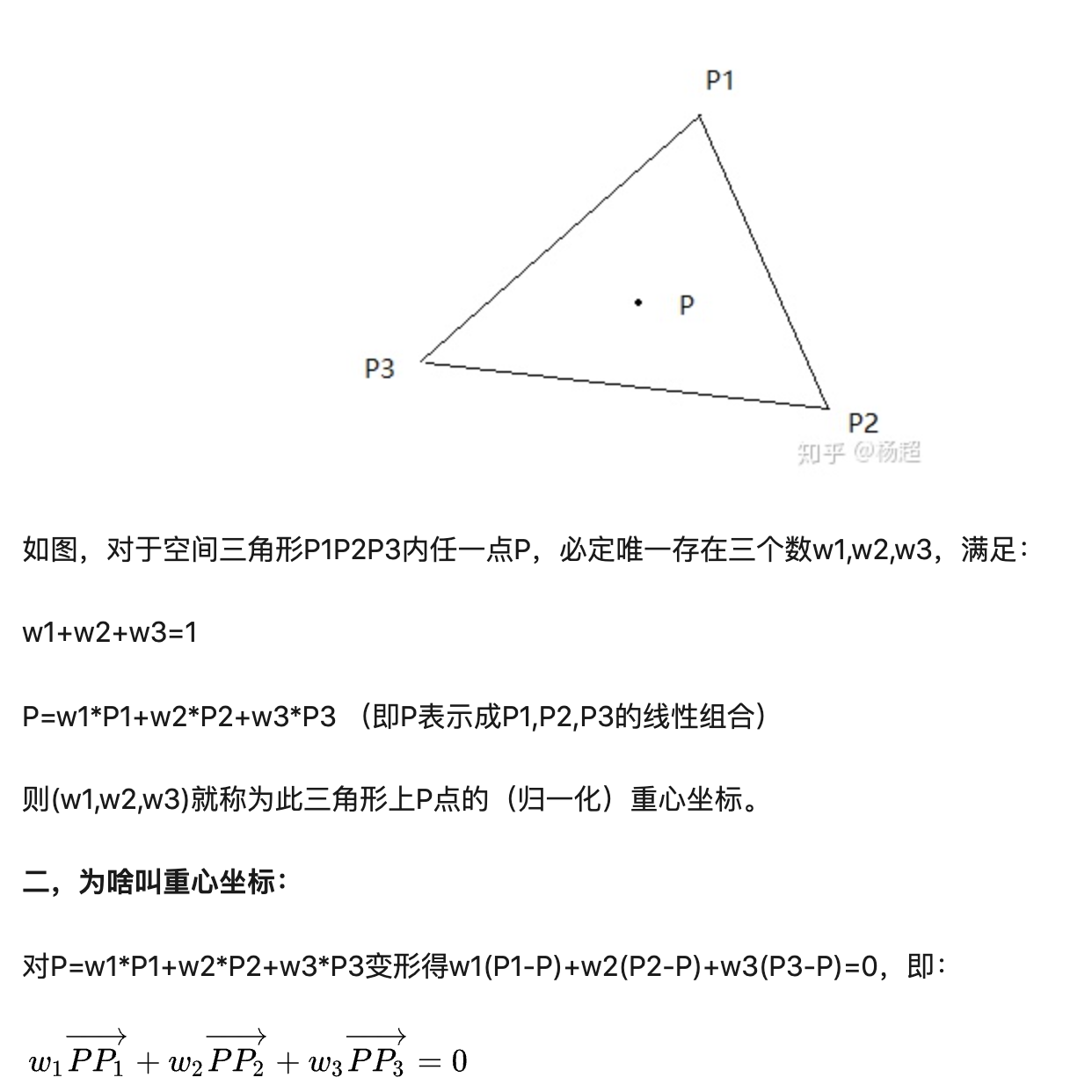
重心坐标

变形得:

计算


这里计算重心坐标时计算了好久,这里记录一下
AP = uAB + vAC
其中 u v 在[0,1]之间
展开:
P-A = u(B-A) + v(C-A)
P = (1-u-v)A + uB + vC
由AP = uAB + vAC
得到
uAB + vAC + PA = 0;
uABx + vACx + PAx = 0;
uABy + vACy + PAy = 0;
正交,实际找到 [ABx, ACx,PAx], [ABy+ ACy + PAy]的叉乘
得到的结果为 [a,b,c]
由于是正交
带入原子式,
aAB + bAC + cPA = 0
展开:
a(B-A) + b(C-A) + c(P-A) = 0;
得到:
P= (1-a/c-b/c)A + a/cB + b/cC
应用
-
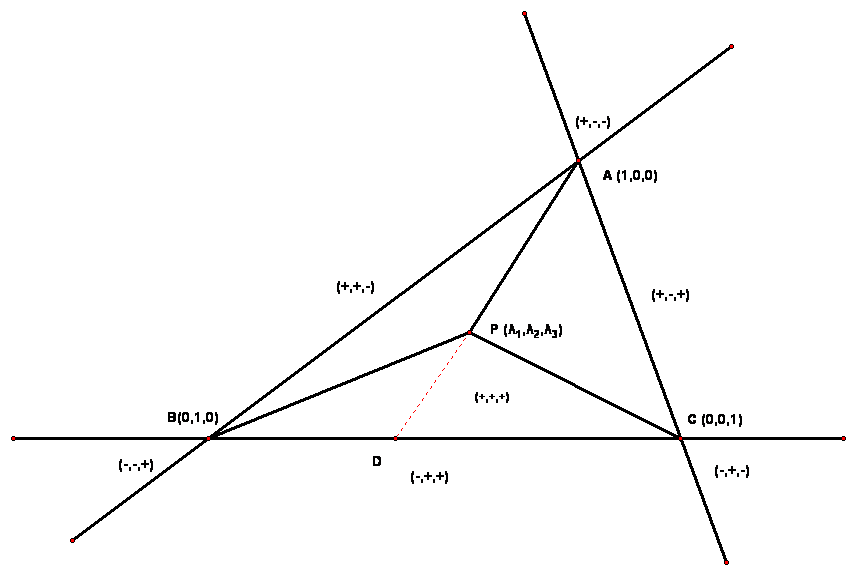
-
P位于三角形ABC内部,u和v必须满足什么条件呢?有如下三个条件
- u >= 0
- v >= 0
- u + v <= 1
几个边界情况,当u = 0且v = 0时,就是点A,当u = 0,v = 1时,就是点B,而当u = 1, v = 0时,就是点C

-
线性插值-纹理等
-
打比方说,P1处纹理坐标为texcoord1,P2处为texcoord2,P3处为texcoord3,则P处纹理坐标就是texcoord=w1texcoord1+w2texcoord2+w3*texcoord3。
-