4.0 坐标系、几何变换
[TOC]
坐标系
参考 维基百科-坐标系
笛卡尔坐标系
二维、三维
x,y,z
齐次坐标
参考字节百科
指的是将一个原本是n维的向量用一个n+1维向量来表示。在几何意义上,相当于把发生在三维空间的变换限制在H=1的平面内。
在齐次坐标表示时,会增加一个额外的坐标,例如平面上的一点可以表示为(x, y, z),其中x/z及y/z为其原来在平面上的笛卡尔坐标。其优点是可以在不使用无限大的情形下表示射影平面上的任意点。一般齐次坐标会用在坐标之间的比例比实际的数值来的重要的情形下。
引入齐次坐标的目的主要是合并矩阵运算中的乘法和加法,改为矩阵乘法。
极坐标系
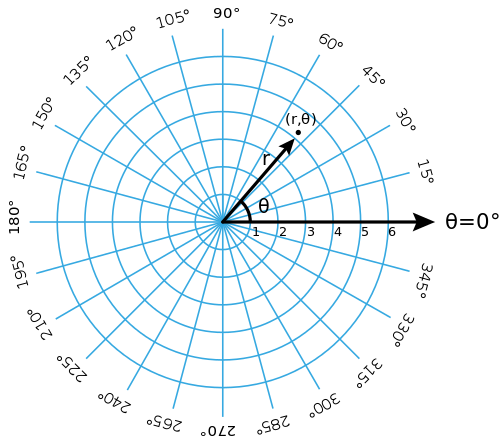
在极坐标系中,一坐标(r, θ)只会其对应唯一的一点,但每一点均可对应许多个坐标。例如坐标(r, θ)、(r, θ+2π)及(−r, θ+π)都是对应同一点的不同坐标。而极点的坐标为(0, θ),θ可为任意值。
球坐标系
利用球坐标(r, θ, φ)表示一个点P在三维空间的位置的三维正交坐标系
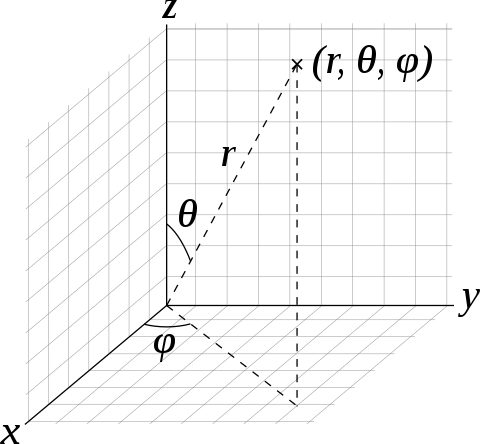
物理学中通常使用的球坐标(r, θ, φ) (ISO 约定):径向距离r,极角θ(theta)与方位角φ(phi)。
其他坐标系
- 曲线坐标系
- 广义坐标
- 正则坐标
- 普吕克坐标
- 重心坐标
- 平行坐标
笛卡尔坐标系下的变换
参考
欧几里得变换
欧几里得变换或欧几里得移动是欧几里得平面的点集到同一平面上点集的(双射)映射,它保持诸点之间的距离。这种映射(也叫等距映射)有四种类型:平移、旋转、反射和滑移反射。
仿射变换
仿射变换,又称仿射映射,是指在几何中,对一个向量空间进行一次线性变换并接上一个平移,变换为另一个向量空间。
在仿射变换中,增加了一个额外维度而所有点对这个额外维度给出数值1。这么做的好处是点平移可以在矩阵A的最后列中指定。在这种方式下,所有欧几里得变换都可处理成矩阵点乘法。
平移
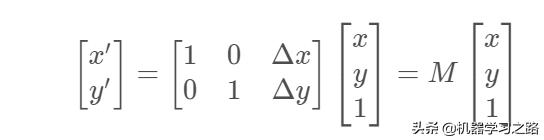
翻转

缩放
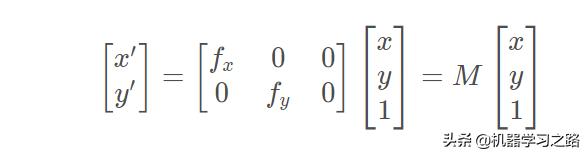
旋转
原点旋转
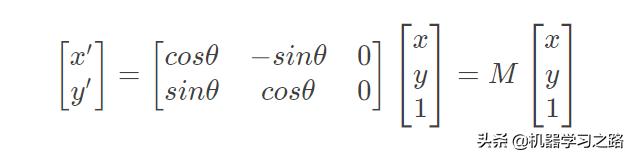
推导
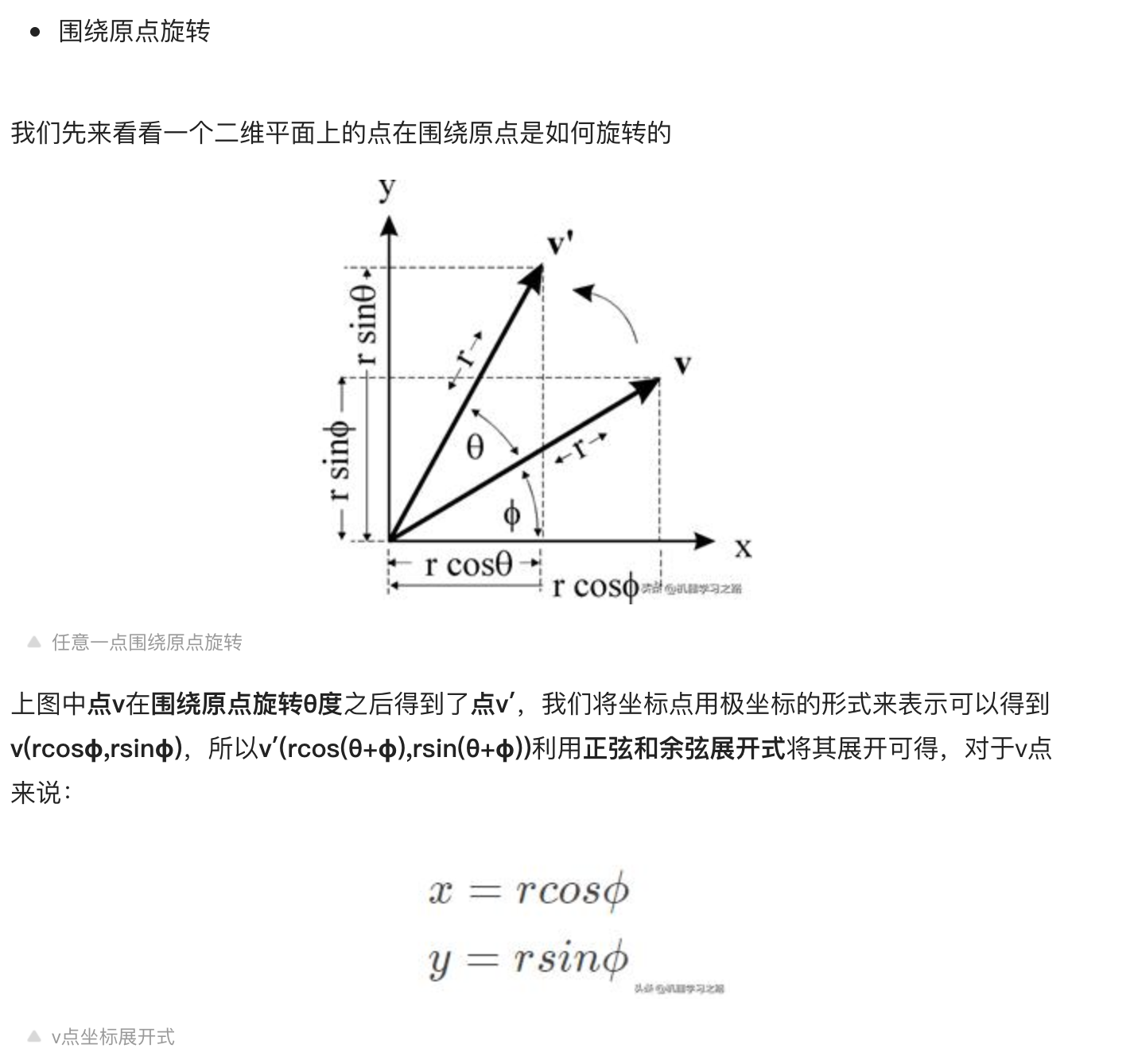

点c(a,b)旋转
