[TOC]

比较好的资料

• 维基百科-欧拉角
• 维基百科-Gimbal lock
• Bonus: Gimbal Lock
  --
• 知乎-如何通俗地解释欧拉角？之后为何要引入四元数？
  --
• 知乎-四元数——基本概念
• 知乎-四元数——旋转
• 知乎-旋转之一复数与2D旋转
• 维基百科-四元数与空间旋转
• 维基百科-四元数

欧拉角

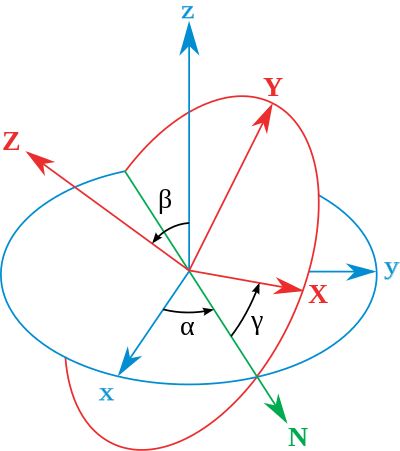
莱昂哈德·欧拉用欧拉角来描述刚体在三维欧几里得空间的取向。换句话说，任何关于刚体旋转的旋转矩阵是由三个基本旋转矩阵复合而成的。

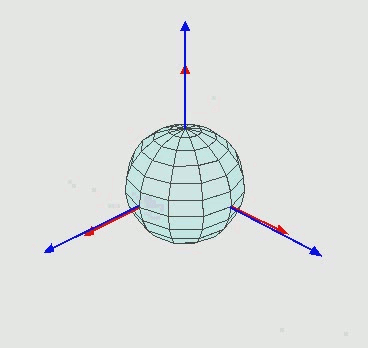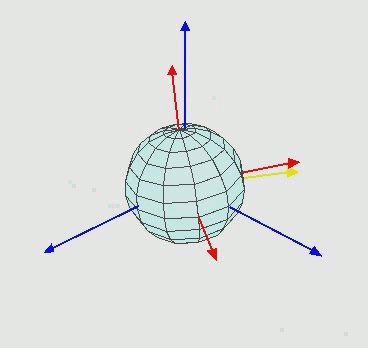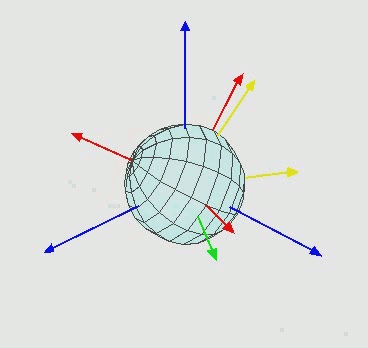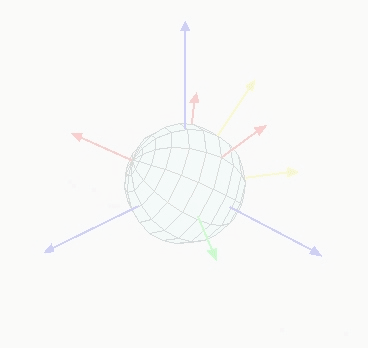
参阅上图。设定xyz-轴为参考系的参考轴。称xy-平面与XY-平面的相交为交点线，用英文字母（N）代表。zxz顺规的欧拉角可以静态地这样定义：

• alpha 是x-轴与交点线的夹角，
• beta 是z-轴与Z-轴的夹角，
• gamma 是交点线与X-轴的夹角。

很可惜地，对于夹角的顺序和标记，夹角的两个轴的指定，并没有任何常规。科学家对此从未达成共识。每当用到欧拉角时，我们必须明确的表示出夹角的顺序，指定其参考轴。

• pitch 俯仰角
  

• yaw 偏航角

• roll 翻滚角

万向锁 gimbal_lock

我的理解，欧拉角之所以自由灵活的转动是因为三个轴不在一个平面上，而像下图，上下翻转90度使得两个轴在一个平面时会发生死锁。

四元数

复数和旋转

复数的矩阵表示

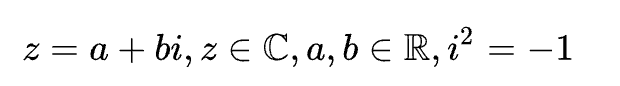
模与共轭

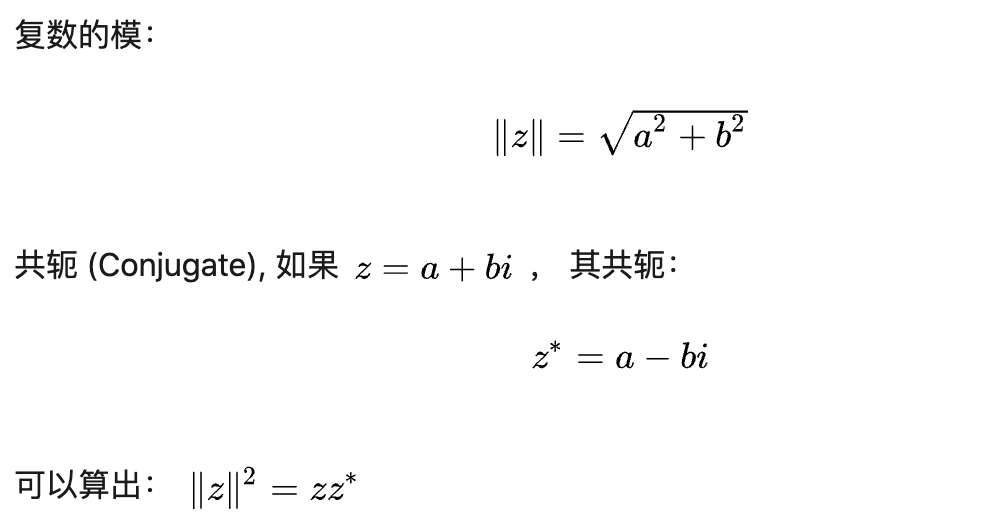
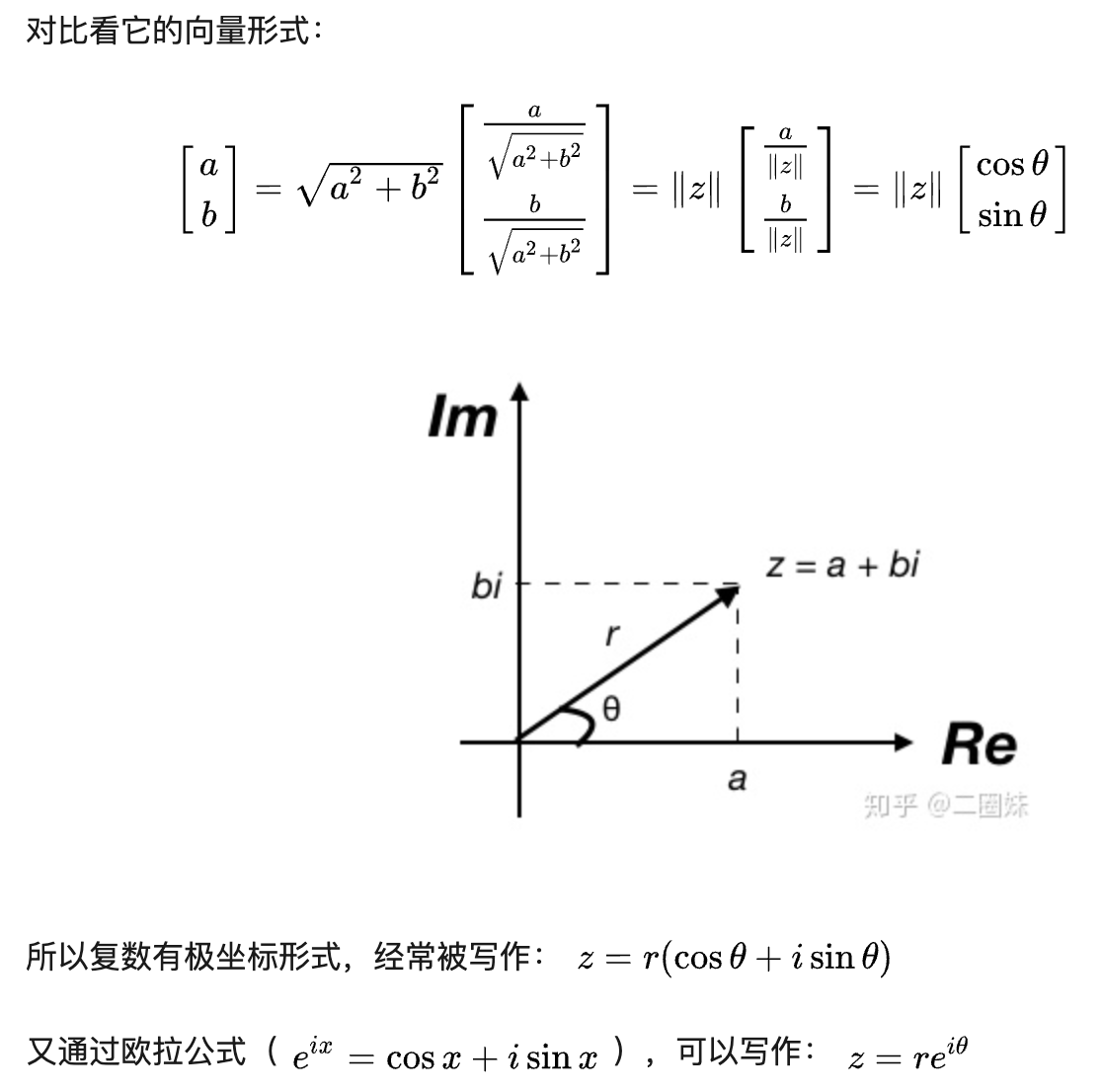
复数的表示方法

复数和旋转

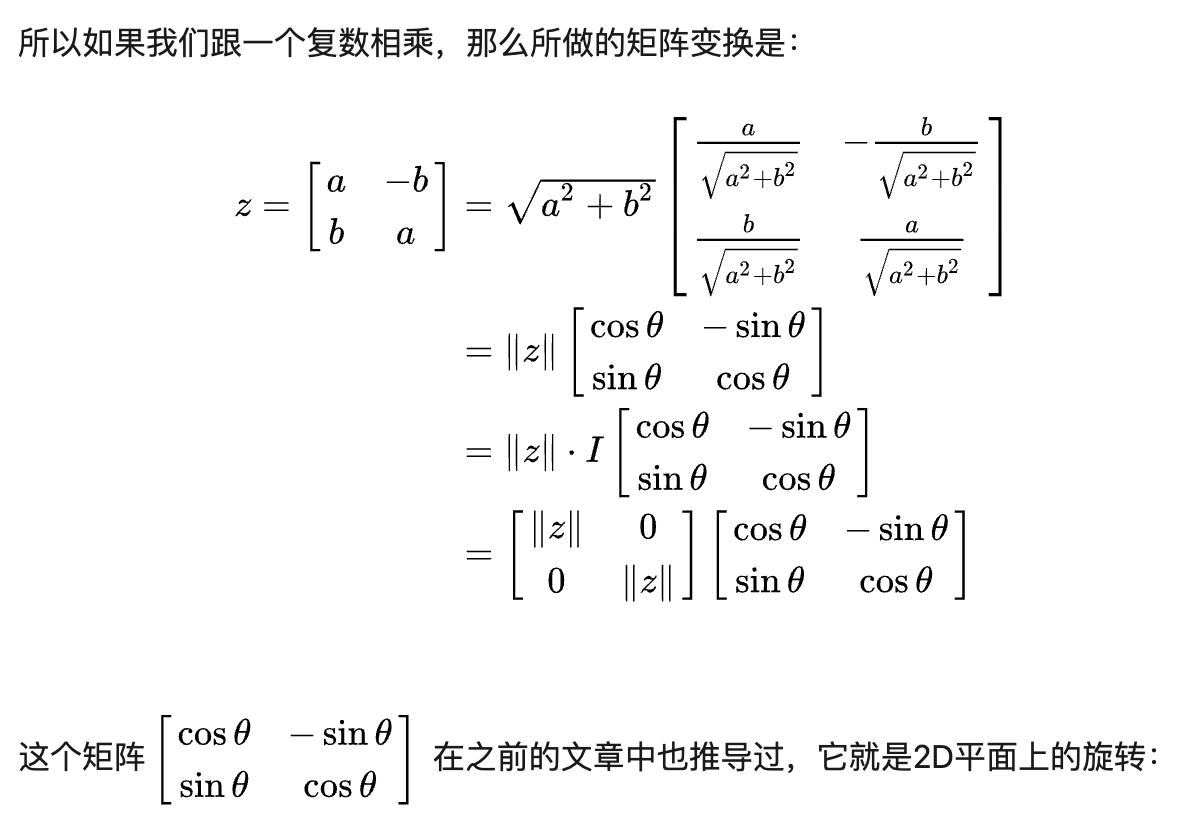
四元数旋转

glm::mat4 model = glm::mat4(1.0f); //创建一个单位矩阵
glm::qua<float> q = glm::qua<float>(glm::radians(glm::vec3(0.0f, 0.0f, 90.0f))); //创建一个绕z轴旋转90度的四元数
model = glm::mat4_cast(q) * model;	//得到一个旋转的模型矩阵